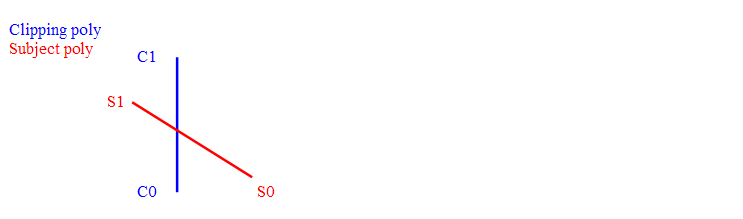Updated on 13/06/2005
I am trying to implement the Weiler Atherton algorithm (You can find the original article here: Weiler Atherton)
The algorithm works well for the general case.
The general case is when intersection points are not on polygon edges (fig 1).
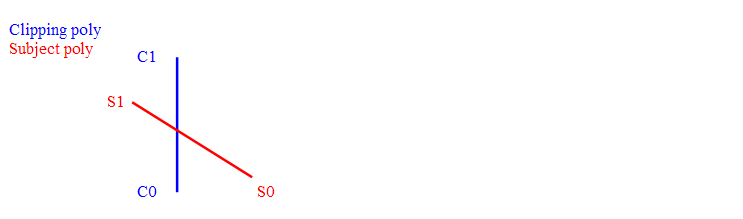
When have then to distinguish two main different non trivial cases
- 1) Two edges intersect on point I and I is on one edge
- 1a) I is not a polygon point (fig 2)
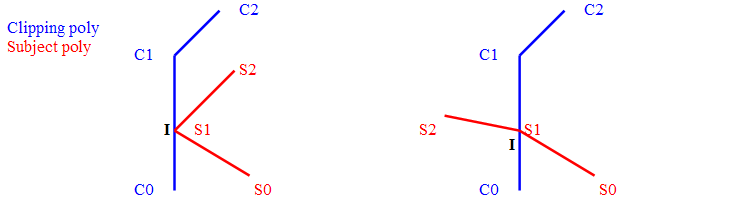
On left side of fig 2, polygons are not crossing. We don't add the I node to the chains and we do as the polygons were not intersecting.
On right side of fig2, polygons are crossing. We add node I to the chains and remove node S1.
- 1b) I is a polygon point (fig 3)
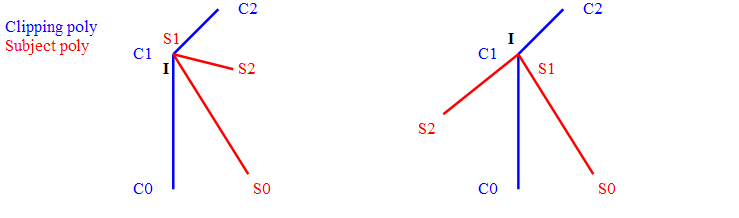
We handle this case as before except that for the crossing subcase, S1 and C1 are removed from the chains.
I did implement the general case and special cases 1a, 1b. It *seems* to works (I didn't get any bugs so far). The number of intersections will always be even and the types will alternate.
I am happy with this until someone finds the breaking case...???
- 2) Two edges intersect, two intersection points (I, J)
I guess there are three cases:
- 2a) I and J are not polygon points (fig 4)

- 2b) I or J is a polygon points (fig 5)

- 2c) I and J are polygon points (fig 6)

For theses cases (2a, 2b, 2c), we track some paths where the 2 polygons are merged. As for first cases, we flag the paths as crossing or not. If a path dont cross, we dont modify
the graph. If it is crossing, we choose one of the intersections points and insert it in the graphs.
This is good because still, the number of intersections will always be even and the types will alternate. That way, cases 1) are just special cases of 2).
So ??? what's next ?
The algorithm works and now i get some errors from .... floating point precisions issues... and that's another story i guess...